(defn logsumexp [& log-vals]
  (let [mx (apply max log-vals)]
    (+ mx
       (Math/log2
	     (apply +
	       (map (fn [z] (Math/pow 2 z))
		    (map (fn [x] (- x mx))
			log-vals)))))))
			
(defn flip [p]
  (if (< (rand 1) p)
    true
    false))

(defn sample-categorical [outcomes params]
  (if (flip (first params))
    (first outcomes)
    (sample-categorical (rest outcomes)
                        (normalize (rest params)))))

(defn score-categorical [outcome outcomes params]
  (if (empty? params)
    (throw "no matching outcome")
    (if (= outcome (first outcomes))
     (Math/log2 (first params))
      (score-categorical outcome (rest outcomes) (rest params)))))

(defn list-unfold [generator len]
  (if (= len 0)
    '()
    (cons (generator)
    (list-unfold generator (- len 1)))))

(defn normalize [params]
  (let [sum (apply + params)]
  (map (fn [x] (/ x sum)) params)))

(defn sample-gamma [shape scale]
(apply + (repeatedly
  shape  (fn []
		     (- (Math/log2 (rand))))
		)))

(defn sample-dirichlet [pseudos]
  (let [gammas (map (fn [sh]
                     (sample-gamma sh 1))
                pseudos)]
    (normalize gammas)))


  

In Natural Languages and Context-Free Languages, we gave an example of a construction—from Swiss German—that could not be captured by a context-free grammar. How are we to capture such structures?

Our motivation for introducing heads, dependents, and argument structure was to capture phrasal dependence between constituents in a sentence. Consider the English verb put. This verb imposes strong phrasal dependence constraints on sentences in which it appears. Usually such sentences must contain phrases expressing: (i) who is doing the putting, (ii) what is being put, and (iii) the destination of the putting event. The sentence John put the loaf of bread is incomplete, while the sentence John put the loaf of bread in his kitchen cupboard is not.

However, natural language also exhibits constituents that do not appear to be required by any head word. Consider the sentence While preparing dinner, John thoughtlessly put the loaf of bread in his kitchen cupboard. In this sentence, the phrases while preparing dinner and thoughtlessly specify additional information about the time and manner of the putting event, but they do not seem to be required by any other constituent. The sentence is well-formed and interpretable without them. Moreover, many (perhaps unboundedly many) modifiers can appear in a sentence. On Tuesday, while preparing dinner, John thoughtlessly put the loaf of bread in his kitchen cupboard without noticing the ants in the honey. Such non-argument phrases are often referred to as modifiers. The critical upshot of the optionality and iterability of modifiers is that they don’t seem to be inserted into the sentences using the same structure-building operations as arguments.

So, for example, it does not seem to make sense to simply list context-free rules which cover all of the cases above.

(def lexicon
     {:S  (list
	   [(li. :S [:N :V]) (/ 1 M)]
	   [(li. :S [:Adv :N :V]) (/ 1 M)]
	   [(li. :S [:Adv :Adv :N :V]) (/ 1 M)]
	   (comment ...) )
      :V  (list
	   [(li. :V ['put :N :N]) (/ 1 N)]
	   [(li. :V ['put :N :N]) (/ 1 N)]
	   [(li. :V ['put :N :N :P])  (/ 1 N)]
	   [(li. :V ['put :N :N :P]) (/ 1 2)]
	   (comment ...))})

If we attempted to cover all possibilities, we would end up with an unboundedly large set of rules!

What we need is a way to add structure without it being specified by lexical heads. A standard way to do this in linguistic is via the use of an operation often called adjunction. Adjunction is thought of as an operation which “squeezes” a node into a derivation tree.

Consider the following pair of trees.

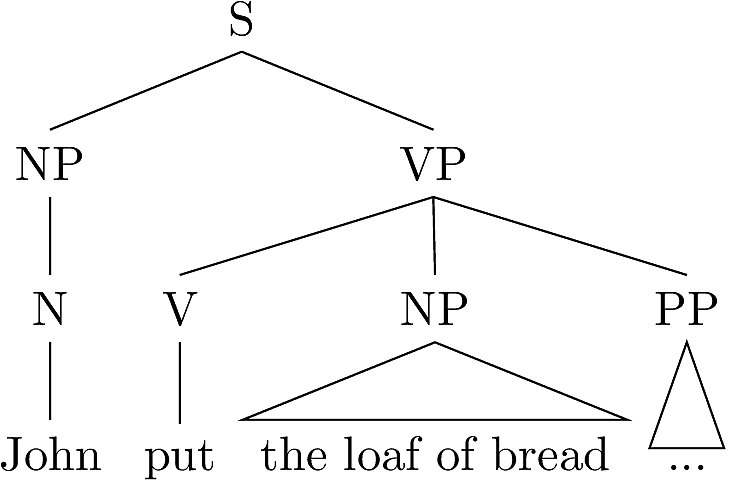
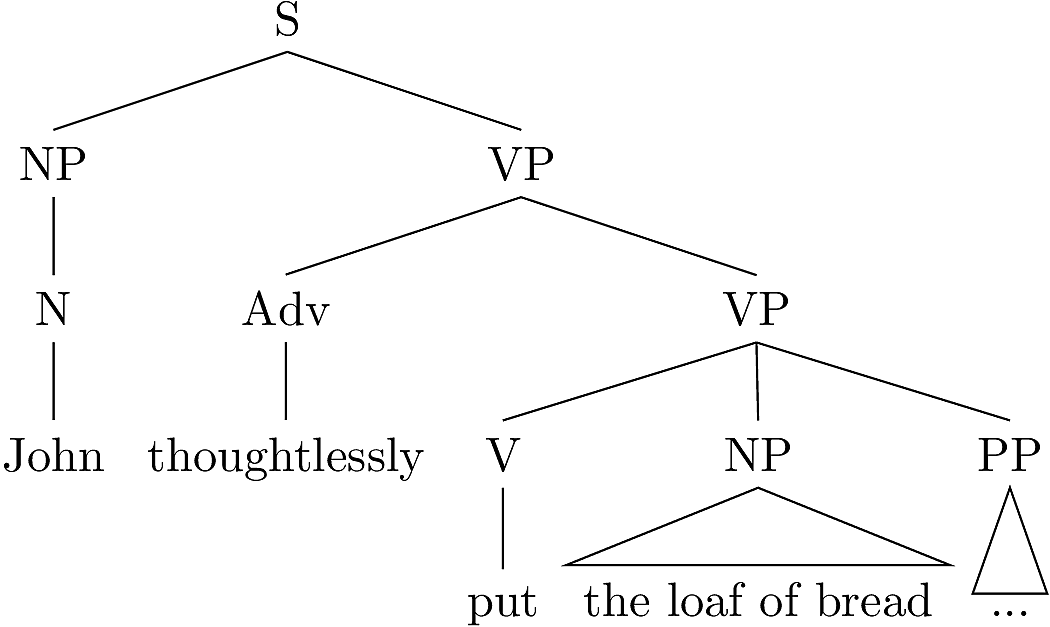
Essentially, we have taken the VP node in the left-hand tree, and squeezed the following tree fragment into it to make the right-hand tree.

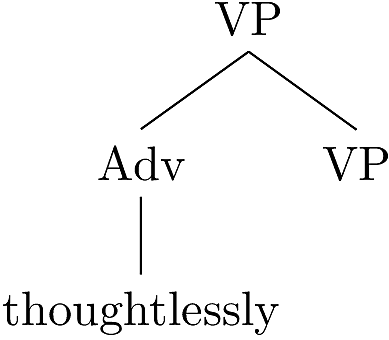
One way of thinking about this is that initial tree is split into a top and bottom component around the VP node and then the adjoined tree is inserted into the middle. The node with the * has been split into a top and bottom component.

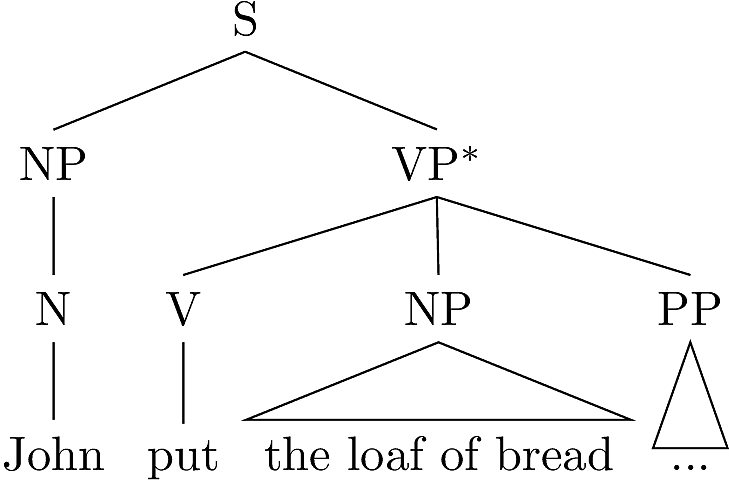
The three components of the new tree are showin below.

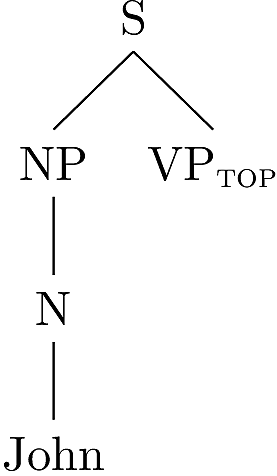
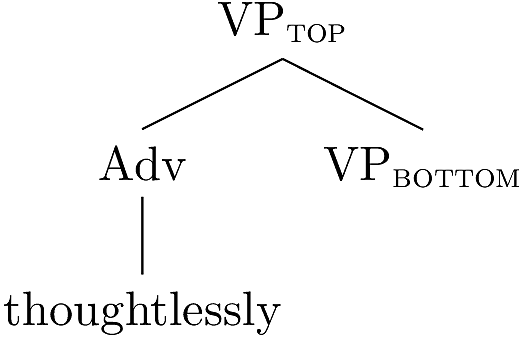
This is a very general operation, which can be schematized as follows.

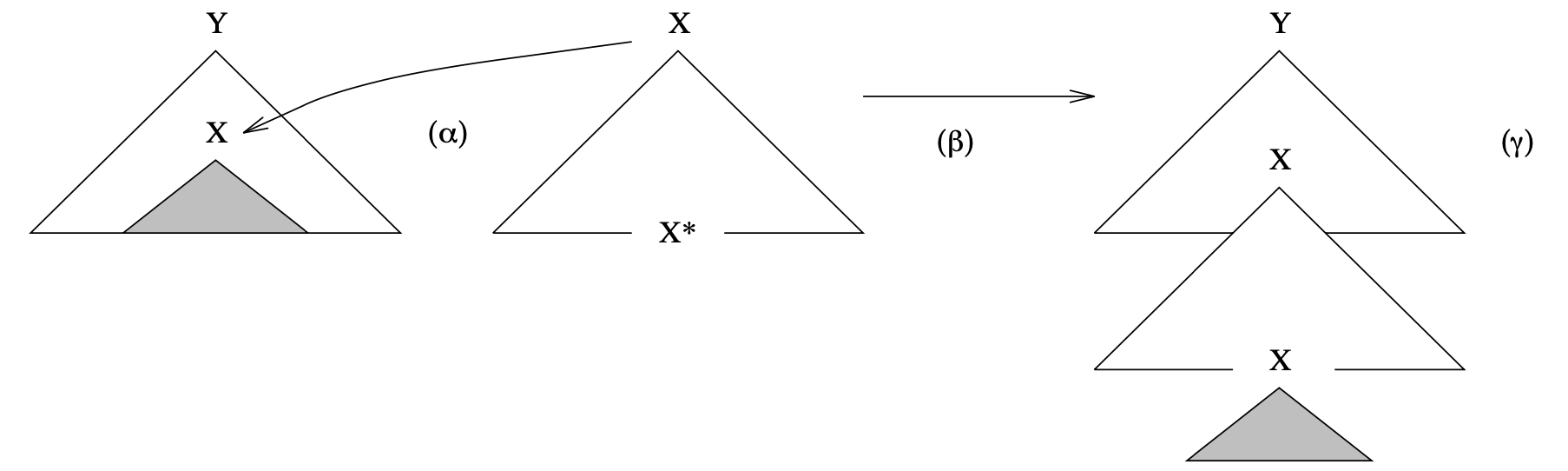
While the operation of adjunction is useful for capturing the distinction between arguments and modifiers, it also gives us a greater degree of formal power. Consider the following fragment of tree structure.

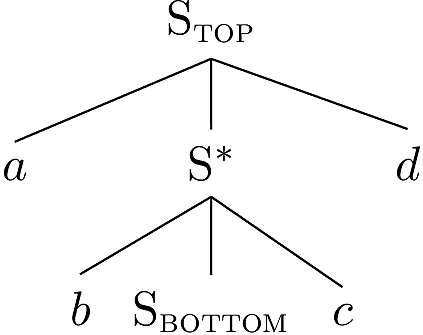
Imagine that this fragment was adjoined into itself at the middle S node. The result would be the following tree.

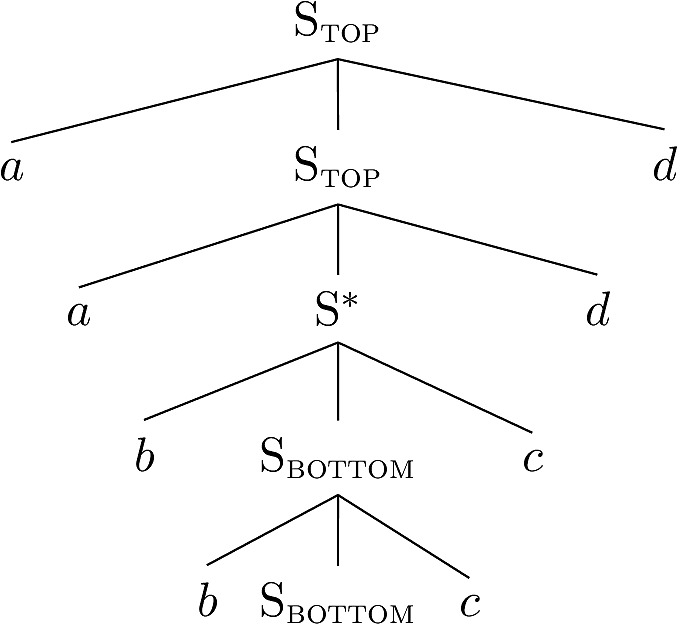
We can adjoin again.

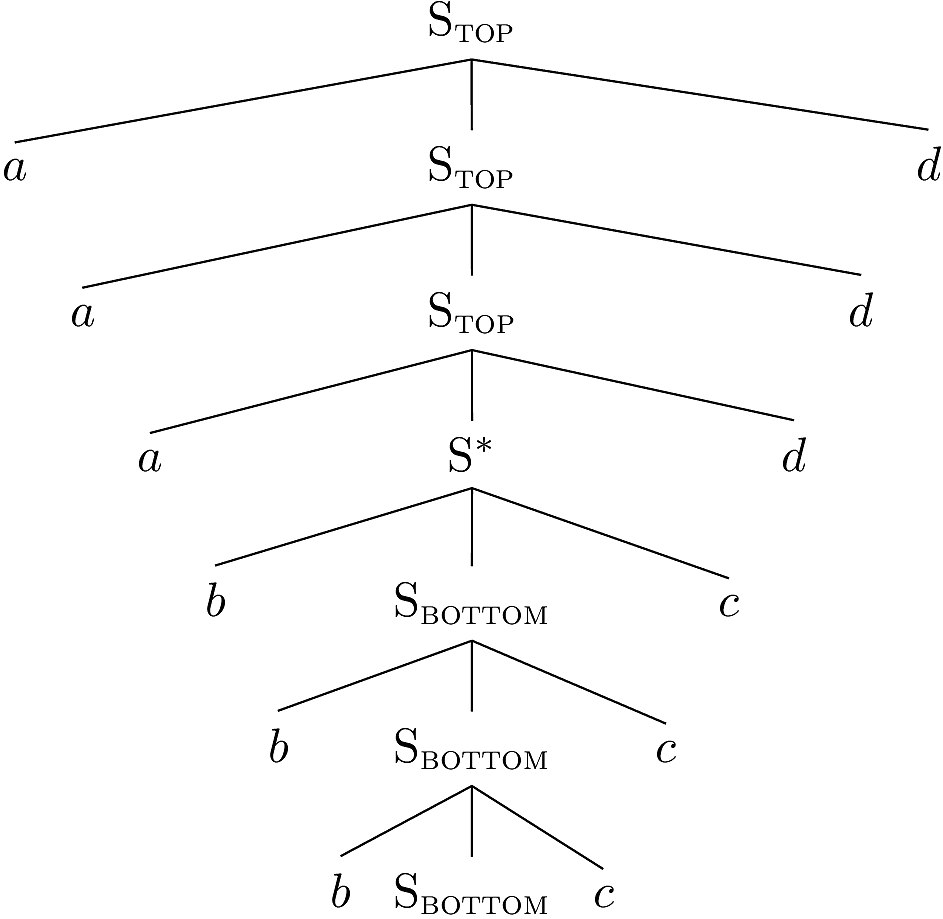
By continually adjoining the tree fragment above into the middle S node, we can generate the language \(a^n b^n c^n d^n\), a non-context-free language.

Let’s turn to the case of Swiss German. Can we use adjunction to model these structures? Consider the following two trees.

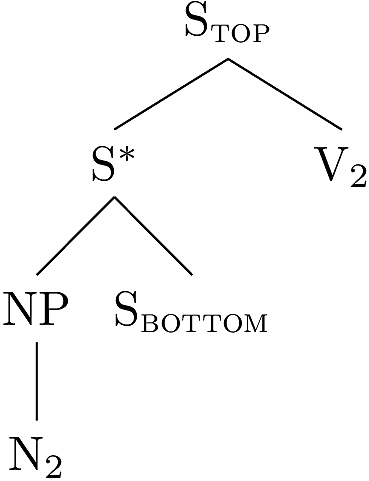
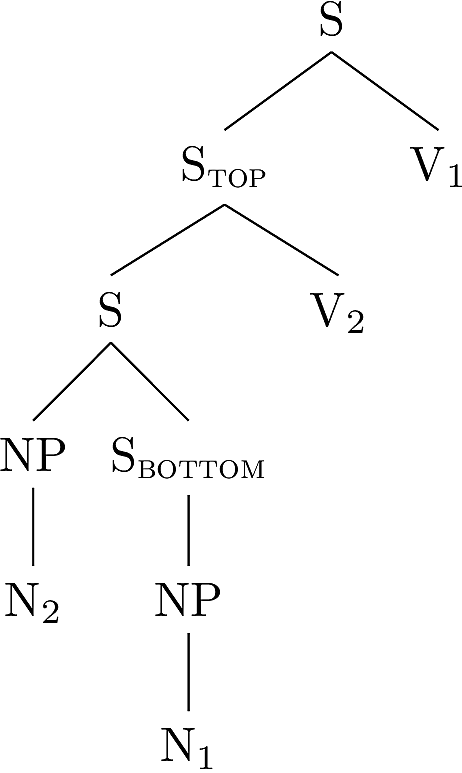
Consider what happens when we adjoin the tree on the right into the three on the left at the starred node.

---

← 50 Natural Languages and Context-Free Languages