(ns foundations.computational.linguistics
(:require [reagent.core :as r]
[reagent.dom :as rd]
[clojure.zip :as z]
[clojure.pprint :refer [pprint]]
[clojure.string :refer [index-of]]
;[clojure.string :as str]
))
(enable-console-print!)
(defn log [a-thing]
(.log js/console a-thing))
(defn render-vega [spec elem]
(when spec
(let [spec (clj->js spec)
opts {:renderer "canvas"
:mode "vega"
:actions {
:export true,
:source true,
:compiled true,
:editor true}}]
(-> (js/vegaEmbed elem spec (clj->js opts))
(.then (fn [res]
(. js/vegaTooltip (vega (.-view res) spec))))
(.catch (fn [err]
(log err)))))))
(defn vega
"Reagent component that renders vega"
[spec]
(r/create-class
{:display-name "vega"
:component-did-mount (fn [this]
(render-vega spec (rd/dom-node this)))
:component-will-update (fn [this [_ new-spec]]
(render-vega new-spec (rd/dom-node this)))
:reagent-render (fn [spec]
[:div#vis])}))
;making a histogram from a list of observations
(defn list-to-hist-data-lite [l]
""" takes a list and returns a record
in the right format for vega data,
with each list element the label to a field named 'x'"""
(defrecord rec [category])
{:values (into [] (map ->rec l))})
(defn makehist-lite [data]
{
:$schema "https://vega.github.io/schema/vega-lite/v4.json",
:data data,
:mark "bar",
:encoding {
:x {:field "category",
:type "ordinal"},
:y {:aggregate "count",
:type "quantitative"}
}
})
(defn list-to-hist-data [l]
""" takes a list and returns a record
in the right format for vega data,
with each list element the label to a field named 'x'"""
(defrecord rec [category])
[{:name "raw",
:values (into [] (map ->rec l))}
{:name "aggregated"
:source "raw"
:transform
[{:as ["count"]
:type "aggregate"
:groupby ["category"]}]}
{:name "agg-sorted"
:source "aggregated"
:transform
[{:type "collect"
:sort {:field "category"}}]}
])
(defn makehist [data]
(let [n (count (distinct ((data 0) :values)))
h 200
pad 5
w (if (< n 20) (* n 35) (- 700 (* 2 pad)))]
{
:$schema "https://vega.github.io/schema/vega/v5.json",
:width w,
:height h,
:padding pad,
:data data,
:signals [
{:name "tooltip",
:value {},
:on [{:events "rect:mouseover", :update "datum"},
{:events "rect:mouseout", :update "{}"}]}
],
:scales [
{:name "xscale",
:type "band",
:domain {:data "agg-sorted", :field "category"},
:range "width",
:padding 0.05,
:round true},
{:name "yscale",
:domain {:data "agg-sorted", :field "count"},
:nice true,
:range "height"}
],
:axes [
{ :orient "bottom", :scale "xscale" },
{ :orient "left", :scale "yscale" }
],
:marks [
{:type "rect",
:from {:data "agg-sorted"},
:encode {
:enter {
:x {:scale "xscale", :field "category"},
:width {:scale "xscale", :band 1},
:y {:scale "yscale", :field "count"},
:y2 {:scale "yscale", :value 0}
},
:update {:fill {:value "steelblue"}},
:hover {:fill {:value "green"}}
}
},
{:type "text",
:encode {
:enter {
:align {:value "center"},
:baseline {:value "bottom"},
:fill {:value "#333"}
},
:update {
:x {:scale "xscale", :signal "tooltip.category", :band 0.5},
:y {:scale "yscale", :signal "tooltip.count", :offset -2},
:text {:signal "tooltip.count"},
:fillOpacity [
{:test "isNaN(tooltip.count)", :value 0},
{:value 1}
]
}
}
}
]
}))
(defn hist [l]
(-> l
list-to-hist-data
makehist
vega))
; for making bar plots
(defn list-to-barplot-data-lite [l m]
""" takes a list and returns a record
in the right format for vega data,
with each list element the label to a field named 'x'"""
(defrecord rec [category amount])
{:values (into [] (map ->rec l m))})
(defn makebarplot-lite [data]
{
:$schema "https://vega.github.io/schema/vega-lite/v4.json",
:data data,
:mark "bar",
:encoding {
:x {:field "element", :type "ordinal"},
:y {:field "value", :type "quantitative"}
}
})
(defn list-to-barplot-data [l m]
""" takes a list and returns a record
in the right format for vega data,
with each list element the label to a field named 'x'"""
(defrecord rec [category amount])
{:name "table",
:values (into [] (map ->rec l m))})
(defn makebarplot [data]
(let [n (count (data :values))
h 200
pad 5
w (if (< n 20) (* n 35) (- 700 (* 2 pad)))]
{
:$schema "https://vega.github.io/schema/vega/v5.json",
:width w,
:height h,
:padding pad,
:data data,
:signals [
{:name "tooltip",
:value {},
:on [{:events "rect:mouseover", :update "datum"},
{:events "rect:mouseout", :update "{}"}]}
],
:scales [
{:name "xscale",
:type "band",
:domain {:data "table", :field "category"},
:range "width",
:padding 0.05,
:round true},
{:name "yscale",
:domain {:data "table", :field "amount"},
:nice true,
:range "height"}
],
:axes [
{ :orient "bottom", :scale "xscale" },
{ :orient "left", :scale "yscale" }
],
:marks [
{:type "rect",
:from {:data "table"},
:encode {
:enter {
:x {:scale "xscale", :field "category"},
:width {:scale "xscale", :band 1},
:y {:scale "yscale", :field "amount"},
:y2 {:scale "yscale", :value 0}
},
:update {:fill {:value "steelblue"}},
:hover {:fill {:value "green"}}
}
},
{:type "text",
:encode {
:enter {
:align {:value "center"},
:baseline {:value "bottom"},
:fill {:value "#333"}
},
:update {
:x {:scale "xscale", :signal "tooltip.category", :band 0.5},
:y {:scale "yscale", :signal "tooltip.amount", :offset -2},
:text {:signal "tooltip.amount"},
:fillOpacity [
{:test "isNaN(tooltip.amount)", :value 0},
{:value 1}
]
}
}
}
]
}))
(defn barplot [l m]
(vega (makebarplot (list-to-barplot-data l m))))
; now, for tree making
;(thanks to Taylor Wood's answer in this thread on stackoverflow:
; https://stackoverflow.com/questions/57911965)
(defn count-up-to-right [loc]
(if (z/up loc)
(loop [x loc, pops 0]
(if (z/right x)
pops
(recur (z/up x) (inc pops))))
0))
(defn list-to-tree-spec [l]
""" takes a list and walks through it (with clojure.zip library)
and builds the record format for the spec needed to for vega"""
(loop [loc (z/seq-zip l), next-id 0, parent-ids [], acc []]
(cond
(z/end? loc) acc
(z/end? (z/next loc))
(conj acc
{:id (str next-id)
:name (str (z/node loc))
:parent (when (seq parent-ids)
(str (peek parent-ids)))})
(and (z/node loc) (not (z/branch? loc)))
(recur
(z/next loc)
(inc next-id)
(cond
(not (z/right loc))
(let [n (count-up-to-right loc)
popn (apply comp (repeat n pop))]
(some-> parent-ids not-empty popn))
(not (z/left loc))
(conj parent-ids next-id)
:else parent-ids)
(conj acc
{:id (str next-id)
:name (str (z/node loc))
:parent (when (seq parent-ids)
(str (peek parent-ids)))}))
:else
(recur (z/next loc) next-id parent-ids acc))))
(defn maketree [w h tree-spec]
""" makes vega spec for a tree given tree-spec in the right json-like format """
{:$schema "https://vega.github.io/schema/vega/v5.json"
:data [{:name "tree"
:transform [{:key "id" :parentKey "parent" :type "stratify"}
{:as ["x" "y" "depth" "children"]
:method {:signal "layout"}
:size [{:signal "width"} {:signal "height"}]
:type "tree"}]
:values tree-spec
}
{:name "links"
:source "tree"
:transform [{:type "treelinks"}
{:orient "horizontal"
:shape {:signal "links"}
:type "linkpath"}]}]
:height h
:marks [{:encode {:update {:path {:field "path"} :stroke {:value "#ccc"}}}
:from {:data "links"}
:type "path"}
{:encode {:enter {:size {:value 50} :stroke {:value "#fff"}}
:update {:fill {:field "depth" :scale "color"}
:x {:field "x"}
:y {:field "y"}}}
:from {:data "tree"}
:type "symbol"}
{:encode {:enter {:baseline {:value "bottom"}
:font {:value "Courier"}
:fontSize {:value 14}
:angle {:value 0}
:text {:field "name"}}
:update {:align {:signal "datum.children ? 'center' : 'center'"}
:dy {:signal "datum.children ? -6 : -6"}
:opacity {:signal "labels ? 1 : 0"}
:x {:field "x"}
:y {:field "y"}}}
:from {:data "tree"}
:type "text"}]
:padding 5
:scales [{:domain {:data "tree" :field "depth"}
:name "color"
:range {:scheme "magma"}
:type "linear"
:zero true}]
:signals [{:bind {:input "checkbox"} :name "labels" :value true}
{:bind {:input "radio" :options ["tidy" "cluster"]}
:name "layout"
:value "tidy"}
{:name "links"
:value "line"}]
:width w}
)
(defn tree-depth
"get the depth of a tree (list)"
[list]
(if (seq? list)
(inc (apply max 0 (map tree-depth list)))
0))
(defn tree
"plot tree using vega"
[list]
(let [spec (list-to-tree-spec list)
h (* 30 (tree-depth list))]
(vega (maketree 700 h spec))))
(defn logsumexp [& log-vals]
(let [mx (apply max log-vals)]
(+ mx
(Math/log2
(apply +
(map (fn [z] (Math/pow 2 z))
(map (fn [x] (- x mx))
log-vals)))))))
(defn flip [p]
(if (< (rand 1) p)
true
false))
(defn sample-categorical [outcomes params]
(if (flip (first params))
(first outcomes)
(sample-categorical (rest outcomes)
(normalize (rest params)))))
(defn score-categorical [outcome outcomes params]
(if (empty? params)
(throw "no matching outcome")
(if (= outcome (first outcomes))
(Math/log2 (first params))
(score-categorical outcome (rest outcomes) (rest params)))))
(defn list-unfold [generator len]
(if (= len 0)
'()
(cons (generator)
(list-unfold generator (- len 1)))))
(defn normalize [params]
(let [sum (apply + params)]
(map (fn [x] (/ x sum)) params)))
(defn sample-gamma [shape scale]
(apply + (repeatedly
shape (fn []
(- (Math/log2 (rand))))
)))
(defn sample-dirichlet [pseudos]
(let [gammas (map (fn [sh]
(sample-gamma sh 1))
pseudos)]
(normalize gammas)))
How can we show that a formal language is not context free. One
important tool for this is the pumping lemma for context-free
languages.
The pumping lemma states that if a language \(L\) is context-free. then there
is a string-length \(l\) such that for any strings \(s\) in the language with
length greater than or equal to \(l\) (i.e., \(|s| \geq l\)), \(s\) can be written
as \(uvwxy\) (i.e., \(s=uvwxy\)) such that \(|vx| \geq 1\) and \(|vwx| \leq l\) and
that all strings \(uv^n wx^n y\) for all \(n\) are also in \(L\).
The intuition behind the pumping lemma is that if a string is long
enough, it must have been generated by recursion and this recursion
can lead to a center-embedding. But if this recursion happened once,
it can happen an unbounded number of times, so whatever material it
adds into the string, it can add into the string some unbounded number
of times.
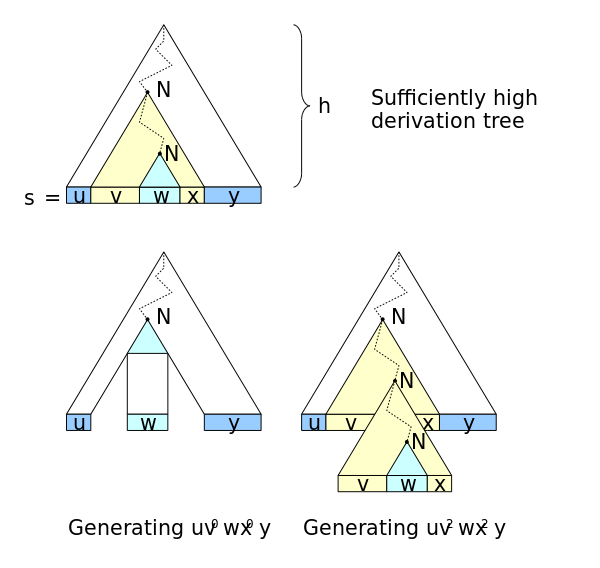
Note that the pumping lemma is not an abstract characterization since
it only provides a necessary, but not a sufficient condition for
membership in the class of context-free languages.
← 48 Parameter Estimation for CFGs
50 Natural Languages and Context-Free Languages →
