← →

31 The Viterbi Algorithm

In this chapter we consider the maximum likelihood solution to the parsing problem for HMMs/FSAs. Recall that the Principle of Maximum Likelihood chooses the single element of the hypothesis space—otherwise known as a point estimate—which maximizes the probability of the data, or the likelihood of the hypothesis. If our hypothesis space is given by \(h \in H\), our data by \(d\) and our (log) likelihood function is given by \(\mathcal{L}(h;d)\) then the principle of maximum likelihood can be expressed as follows.

\[\DeclareMathOperator*{\argmax}{arg\,max} \hat{h} = \underset {h \in H }\argmax \mathcal{L}(h;d)\]

The joint probability of a sequence of words and categories under a Hidden Markov Model is given by

\[\Pr(w^{(1)},\dots,w^{(k)},c^{(1)},\cdots,c^{(k)})=\prod_{i=1}^k \Pr(w^{(i)} \mid c^{(i)}) \Pr(c^{(i)} \mid c^{(i-1)})\]

We seek to find a sequence of categories \(\hat{c}^{(1)},\cdots,\hat{c}^{(k)}\) which maximizes this expression.

\[\DeclareMathOperator*{\argmax}{arg\,max} \hat{c}^{(1)},\cdots,\hat{c}^{(k)} = \underset {c^{(1)},\cdots,c^{(k)} }\argmax \prod_{i=1}^k \Pr(w^{(i)} \mid c^{(i)}) \Pr(c^{(i)} \mid c^{(i-1)}) \}\]

Note that each term in the expression above, depends on the preceding category. Thus, in order to maximize the expression, we will need to perform a search over all sequences of categories, of which there are exponentially many. However, as was the case with computing the marginal or forward probability of a string under an HMM, we can make use of the conditional independence assumptions of the model to derive a more efficient algorithm. The resulting algorithm is known as the Viterbi algorithm.

Let’s define a function, \(\mathbf{vt}\) which returns the probability of the sequence of categories that maximizes the likelihood of some sequence of observed words and ends in state \(c^{(k)}\). This probability is called the Viterbi score of the sequence. Note that here we are using the \(\max\) function, rather than the \(\argmax\) function.

\[\begin{align}\mathbf{vt}(w^{(1)},\cdots,w^{(k)}, c^{(k)}) &=& & \underset {c^{(1)},\cdots,c^{(k-1)}}\max \Pr(w^{(1)},\dots, w^{(k)}, c^{(1)},\cdots, c^{(k-1)}, c^{(k)})\\ \end{align}\]

Importantly, in the expression above, the \(max\) ranges over all of the states up to state \(c^{(k)}\) but not including it, since it is fixed. We can use the conditional independence assumption of the HMM to decompose the expression above into two parts. One which maximizes the final transition to \(c^{(k)}\) and one which maximizes the earlier state sequence.

\[\begin{align} \mathbf{vt}(w^{(1)},\cdots,w^{(k)},c^{(k)}) &=& \Pr(w^{(k)}|c^{(k)}) \underset {c^{(k-1)}}\max \{ \Pr(c^{(k)}|c^{(k-1)}) & \underset {c^{(1)},\cdots,c^{(k-2)}}\max \Pr(w^{(1)},\dots, w^{(k-1)},c^{(1)},\cdots, c^{(k-2)},c^{(k-1)}) \} \\ \mathbf{vt}(w^{(1)},\cdots,w^{(k)},c^{(k)}) &=& \Pr(w^{(k)}|c^{(k)}) \underset {c^{(k-1)}}\max \{ \Pr(c^{(k)}|c^{(k-1)}) & \mathbf{vt}(w^{(1)},\cdots,w^{(k-1)},c^{(k-1)}) \} \end{align}\]

Thus, the Viterbi score can be computed efficiently in a way analogous to the inside probability, just by replacing the sums in the definition of the inside score with \(\max\).

From the perspective of the trellis, we simply store the score of the best path into each node, rather than the sum probability of all paths into the node.

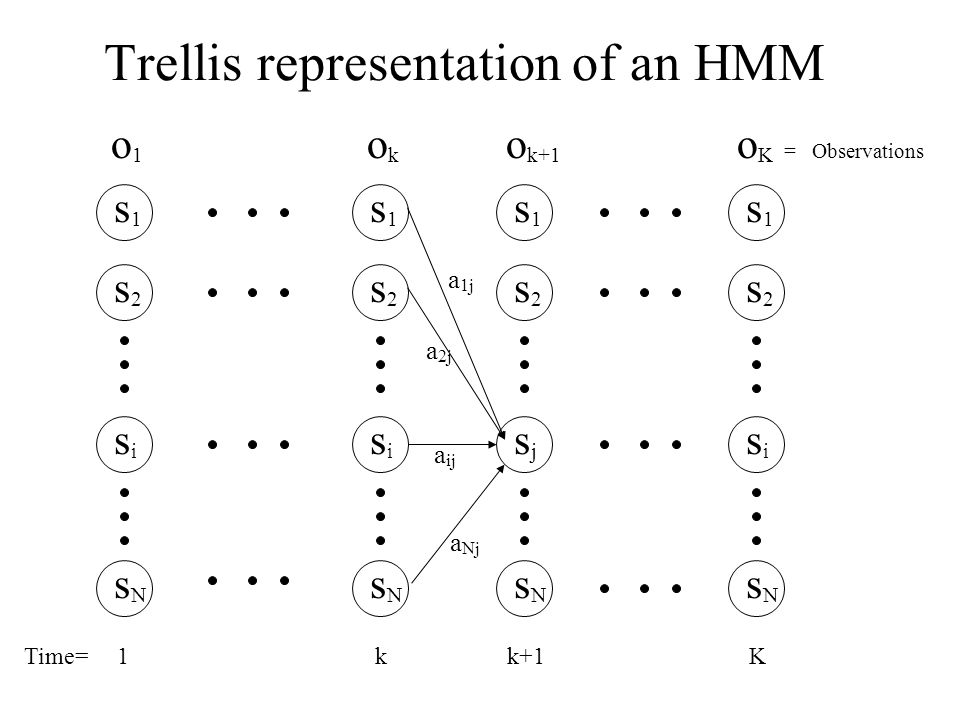
trellis

What does this look like in code? First, let’s remind ourselves what the sampler for an HMM looks like.

(def categories '(N V Adj Adv P stop))

(def vocabulary '(Call me Ishmael))

(def category->transition-probs
  (memoize (fn [category]
             (sample-dirichlet
              (repeat (count categories) 1)))))

(defn sample-category [preceding-category]
  (sample-categorical
   categories
   (category->transition-probs preceding-category)))

(def category->observation-probs
  (memoize (fn [category]
             (sample-dirichlet
              (repeat (count vocabulary) 1)))))

(defn sample-observation [category]
  (sample-categorical
   vocabulary
   (category->observation-probs category)))

(defn sample-categories-words [preceding-category]
  (let [c (sample-category preceding-category)]
    (if (= c 'stop)
      '()
      (cons
       [c (sample-observation c)]
       (sample-categories-words c)))))

(sample-categories-words 'start)

Given this sampler, we can now define a function which computes the Viterbi score of a sequence and a state.

(defn viterbi-score [category sentence]
  (if (empty? sentence)
    0
    (+ 
     (apply 
      max
      (map (fn [c]
             (+ (viterbi-score c (all-but-last sentence))
                (score-categorical 
                 c categories 
                 (category->transition-probs c))))
           categories))
     (if (= category 'stop)
       0
       (score-categorical
        (last sentence) vocabulary
        (category->observation-probs category))))))

(viterbi-score 'stop '(Call me Ishmael))

← 30 Parsing and Inference 32 Bayesian Parsing Methods →