(defn logsumexp [& log-vals]
  (let [mx (apply max log-vals)]
    (+ mx
       (Math/log2
	     (apply +
	       (map (fn [z] (Math/pow 2 z))
		    (map (fn [x] (- x mx))
			log-vals)))))))
			
(defn flip [p]
  (if (< (rand 1) p)
    true
    false))

(defn sample-categorical [outcomes params]
  (if (flip (first params))
    (first outcomes)
    (sample-categorical (rest outcomes)
                        (normalize (rest params)))))

(defn score-categorical [outcome outcomes params]
  (if (empty? params)
    (throw "no matching outcome")
    (if (= outcome (first outcomes))
     (Math/log2 (first params))
      (score-categorical outcome (rest outcomes) (rest params)))))

(defn normalize [params]
  (let [sum (apply + params)]
  (map (fn [x] (/ x sum)) params)))

(defn sample-gamma [shape scale]
(apply + (repeatedly
  shape  (fn []
		     (- (Math/log2 (rand))))
		)))

(defn sample-dirichlet [pseudos]
  (let [gammas (map (fn [sh]
                     (sample-gamma sh 1))
                pseudos)]
				(normalize gammas)))

(defn update-context [order old-context new-symbol]
  (if (>= (count old-context) order)
    (throw "Context too long!")
    (if (= (count old-context) (- order 1))
      (concat  (rest old-context) (list new-symbol))
      (concat old-context (list new-symbol)))))

(defn hmm-unfold [transition observation order context current stop?]
  (if (stop? current)
    (list current)
    (let [new-context (update-context
	           order
		       context
		       current)
	        nxt (transition new-context)]
	  (cons [current (observation current)]
	  (hmm-unfold
	         transition
	         observation
	         n-gram-order 
			 new-context
			 nxt
			 stop?)))))

  

We have a similar problem with scoring HMMs that we did with the categorical bag of words model we looked at earlier. We need to sum over every possible sequences of hidden categories (states) that could have produced the sentence in question. In other words, we need to compute the following marginal.

\[\Pr(w^{(1)},\dots,w^{(k)},C^{(k+1)}=\ltimes) = \sum_{c^{(1)}\in \mathcal{S}} \cdots \sum_{c^{(k)}\in \mathcal{S}} \Pr(w^{(1)},\dots,w^{(k)}, c^{(1)},\dots,c^{(k)},C^{(k+1)}=\ltimes)\]

Substituting in the definition of an HMM, including correctly handling transitions from the start \(\rtimes\) and stop \(\ltimes\) symbols we get.

\[\begin{multline} \Pr(w^{(1)},\dots,w^{(k)},C^{(k+1)}=\ltimes)=\\ \sum_{c^{(1)}\in \mathcal{S}} \cdots \sum_{c^{(k)} \in \mathcal{S}} \Pr(w^{(1)} \mid c^{(1)}) \Pr(c^{(1)} \mid \rtimes) \Big[ \prod_{i=2}^k \Pr(w^{(i)} \mid c^{(i)}) \Pr(c^{(i)} \mid c^{(i-1)}) \Big] \Pr(\ltimes \mid c^{(k)}) \end{multline}\]

Unfortunately, because the terms for the state probabilities at each word are no longer independent of their position in the string, we won’t be able to factorize as aggressively as we could in the categorical bag of words model. However, we can still do some rearranging in this model to achieve an efficient algorithm.

We do this in two steps. First, we note that the probability above represents the marginal probability of the words \(w^{(1)},\dots,w^{(k)}\) and the HMM transitioning after all of these words into the stop state \(\ltimes\). We first generalize this idea and consider the marginal probability of \(j\) words and the HMM then transitioning to an arbitrary state \(c^{(j+1)}\) in the next time step (rather than necessarily \(\ltimes\)).

This can be expressed as a sum over all possible state sequences up to time step \(j\) with a final transition to \(c^{(j+1)}\).

\[\begin{multline} \Pr(w^{(1)},\dots,w^{(j)},c^{(j+1)})=\\ \sum_{c^{(1)}\in \mathcal{S}} \cdots \sum_{c^{(j)} \in \mathcal{S}} \Pr(w^{(1)} \mid c^{(1)}) \Pr(c^{(1)} \mid \rtimes) \Big[\prod_{i=2}^j \Pr(w^{(i)} \mid c^{(i)}) \Pr(c^{(i)} \mid c^{(i-1)})\Big] \Pr(c^{(j+1)} \mid c^{(j)}) \end{multline}\]

The products inside the outer sums here can be grouped according to their final state \(c^{(j)}\) into \(|\mathcal{S}|\) groups that share the factor \(\Pr(c^{(j+1)} \mid c^{(j)}) \Pr(w^{(j)} \mid c^{(j)})\). We pull this factor out.

\[\begin{multline} \phantom{\Pr(w^{(1)},\dots,w^{(j)},c^{(j+1)})}=\\ \sum_{c^{(j)}\in \mathcal{S}} \bigg[\Pr(c^{(j+1)} \mid c^{(j)}) \Pr(w^{(j)} \mid c^{(j)})~\cdot\\ \sum_{c^{(1)}\in \mathcal{S}} \cdots \sum_{c^{(j-1)} \in \mathcal{S}} \Pr(w^{(1)} \mid c^{(1)}) \Pr(c^{(1)} \mid \rtimes) \Big[\prod_{i=2}^{j-1} \Pr(w^{(i)} \mid c^{(i)}) \Pr(c^{(i)} \mid c^{(i-1)}) \Big] \Pr(c^{(j)} \mid c^{(j-1)})\bigg] \end{multline}\]

Now, however, the term on the final line is simply an analogous probability to the one we started with, except one state back, that is, \(\Pr(w^{(1)},\dots,w^{(j-1)},c^{(j)})\).

\[\begin{multline} \phantom{\Pr(w^{(1)},\dots,w^{(j)},c^{(j+1)})}=\\ \sum_{c^{(j)}\in \mathcal{S}} \bigg[\Pr(c^{(j+1)} \mid c^{(j)}) \Pr(w^{(j)} \mid c^{(j)})~\cdot\\ \Pr(w^{(1)},\dots,w^{(j-1)},c^{(j)})\bigg] \end{multline}\]

In the theory of hidden Markov models, this quantity has a special name. It is called the forward probability of state \(c^{(j+1)}\)

\[\mathbf{fw}_{j}(c^{(j+1)}) := \Pr(w^{(1)},\dots,w^{(j)},c^{(j+1)})\]

Using the forward probability, we can write the recurrence above more compactly, with the base case $\mathbf{fw}_{0}(c^{(1)}) = \Pr(c^{(1)}\mid \rtimes)$.

\[\begin{align} \mathbf{fw}_{j}(c^{(j+1)}) = \sum_{c^{(j)} \in \mathcal{S}} \left[ \mathbf{fw}_{j-1}(c^{(j)}) \cdot \Pr(w^{(j)} \mid c^{(j)}) \Pr( c^{(j+1)} \mid c^{(j)}) \right] \end{align}\]

Now, in order to compute the target marginal probability of our length-$k$ sentence, we need only compute \(\mathbf{fw}_{k}(\ltimes)\), the probability of observing words $w^{(1)},\ldots,w^{(k)}$ and then transitioning to the stop state.

It is helpful to visualize the computation of the forward probabilities using the trellis datastructure.

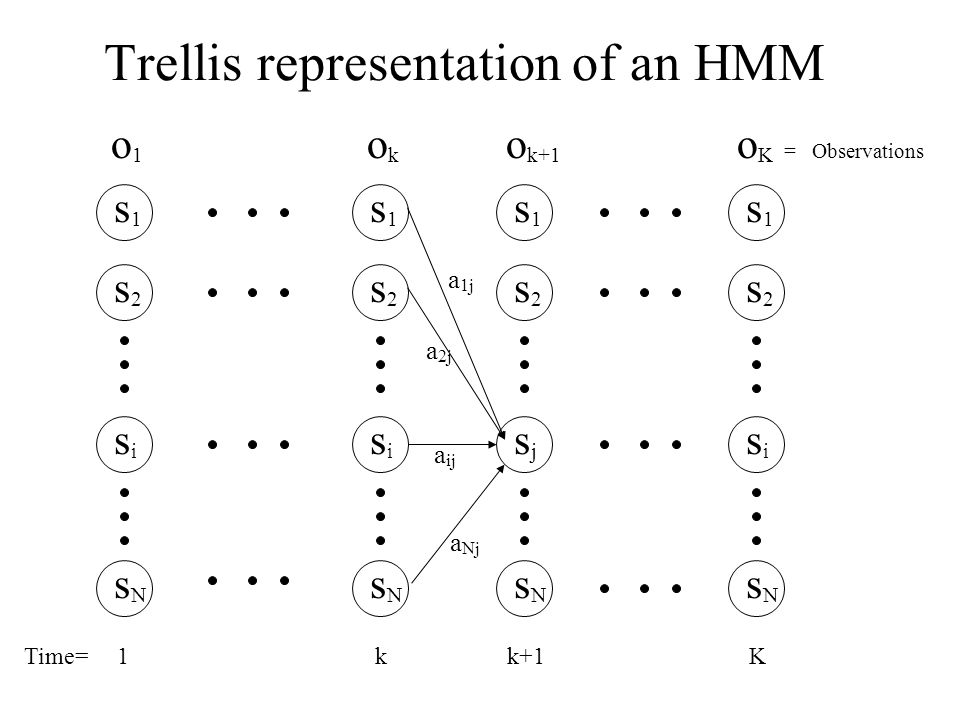
Let’s see how we can write the recursion in the forward algorithm as a function. First, let’s repeat the definitions of our HMM, for reference.

(def categories '(N V Adj Adv P stop))

(def vocabulary '(Call me Ishmael))

(def category->transition-probs
  (memoize (fn [category]
             (sample-dirichlet
              (repeat (count categories) 1)))))

(defn sample-category [preceding-category]
  (sample-categorical
   categories
   (category->transition-probs preceding-category)))

(def category->observation-probs
  (memoize (fn [category]
             (sample-dirichlet
              (repeat (count vocabulary) 1)))))

(defn sample-observation [category]
  (sample-categorical
   vocabulary
   (category->observation-probs category)))

Now, we will need a function which can drop the last element from a list. This is similar the rest function, except it works from the end of the list.

(defn all-but-last [l] 
  (if (empty? (rest l)) 
    '()
    (cons (first l) (all-but-last (rest l)))))

(all-but-last '(1 2 3))

Finally, we are in a position to implement our forward probability recursion as a Clojure function.

(defn score-word-and-transition [category next-category word]
  (+ 
   (score-categorical next-category categories 
                      (category->transition-probs category))
   (score-categorical word vocabulary 
                      (category->observation-probs category))))

(defn forward-probability [next-category sentence]
  (if (empty? sentence)
    (score-categorical next-category categories 
                       (category->transition-probs 'start))
    (apply 
     logsumexp
     (map (fn [c]  
            (+ 
             (forward-probability c (all-but-last sentence))
             (score-word-and-transition c next-category (last sentence))
             ))
          categories))))

(forward-probability 'stop '(Call me Ishmael))

However, we still have a problem. What is the run time of the recursion above? Note that it produces a separate sequence of categories for each path backwards through the string. In other words, it is enumerating all possible sequences of categories (exponentially many), rather than taking advantage of the structure of the recursion we defined above. Thus runtime scales exponentially in the length of the sentence.

(time
 (forward-probability
  'stop 
  '(Ishmael Call me)))

(time
 (forward-probability
  'stop 
  '(me Ishmael me Call Ishmael me)))

We already have a tool that can be used to fix this: memoization. Let’s define a memoized version of the above function.

(def forward-probability-memoized 
  (memoize
   (fn [next-category sentence]
     (if (empty? sentence)
       (score-categorical next-category categories
                          (category->transition-probs 'start))
       (apply 
        logsumexp
        (map (fn [c]  
               (+ 
                (forward-probability-memoized c (all-but-last sentence))
                (score-word-and-transition c next-category (last sentence))))
             categories))))))
		
(forward-probability-memoized 'stop '(Call me Ishmael))

The memoized version takes advantage of the recursion to be much more efficient.

(time
 (forward-probability-memoized 
  'stop 
  '(Ishmael Call me)))

(time
 (forward-probability-memoized 
  'stop 
  '(me Ishmael me Call Ishmael me)))

---

← 24 Hidden Markov Models 26 The Backward Algorithm →