19 Dependencies between Words
(defn prefix? [pr str]
(if (> (count pr) (count str))
false
(if (empty? pr)
true
(if (= (first pr) (first str))
(prefix? (rest pr) (rest str))
false))))
In the last few units, we have studied the categorical bag of words model, including how to choose from models in this class using the principle of maximum likelihood and Bayesian inference. Let’s return back to our overall goal for the course, which was to build models that can distinguish strings of words that are grammatical from those that are not, such as in the following cases.
Colorless green ideas sleep furiously.
\(^*\)Furiously sleep ideas green colorless.
Bag-of-word models necessarily generate every possible sequence of words over the subset of the vocabulary that they put mass on (i.e., \(V^*\) if they put \(>0\) probability on all elements of \(V\).) Thus, if they put probability mass on one of the two strings above, they must put probability mass on both. This is clearly undesirable.
What can we add to our models to allow them to distinguish between these two cases? Intuitively and at a minimum, a model of natural language syntax needs to capture some notion of dependence between words. For instance, there is a dependency between the word word green and the word ideas in the grammatical sentence above. Green is an adjective which modifies the noun ideas. In this unit, we will introduce one of the simplest models of dependencies between words, \(n\)-gram models, also known as Markov models.
N-gram Models and Strictly-Local Languages
One simple kind of dependency between words are adjacent dependencies—co-occurrence constraints between sequences of words that occur next to one another. One idea for how to define a grammar that constrains possible and impossible adjacent dependencies is by simply listing the sequences of adjacent words that are allowed.
We begin with a finite set of constraints of finite length sequences of words known as n-grams (in probabilistic modeling) or n-factors (in formal language theory).
An \(n\)-gram (\(n\)-factor) is a length \(n\) sequence of words over some vocabulary \(V\). Length \(2\) \(n\)-grams are called bigrams, length \(3\) \(n\)-grams are called trigrams and longer \(n\)-grams are usually labeled with \(n\) (e.g., \(5\)-grams). Thus, if our vocabulary is \(V=\{a,b\}\) the set of possible bigrams is \(\{aa,bb,ab,ba\}\), the set of possible trigrams is \(\{aaa,abb,aba,aab,baa,bbb,bba,bab\}\) and so on.
An n-gram-model is a model of strings where we use \(n\)-grams to encode dependencies between adjacent words. In particular, an \(n\)-gram captures the idea that the \(n\)th word depends on the \((n-1)\) words that precede it. A strictly-local language is a language that is definable by an \(n\)-gram model.
Strictly Local Languages
We have spent a considerable amount of time exploring various notions from probability theory. We now return to the formal language theoretic foundations of our discipline. How can we define the formal languages associated with a set of \(n\)-grams? Recall that we introduced two different ways of characterizing formal languages—using generators or recognizers. First, however, we need some way of talking formally about the \(n\)-grams themselves.
Factors
Let \(\mathbf{F}_n(s)\) be a function which returns the set of length \(n\) substrings, that is the n-grams or n-factors of a given string \(s\). If \(|s|<n\) then \(\mathbf{F}_n\) just returns the whole string.
For example:
\[\begin{aligned} \mathbf{F}_2(\rtimes abab\ltimes) &=& \{\rtimes a,ab,ba,b\ltimes\} \\ \mathbf{F}_3(\rtimes abab\ltimes) &=& \{\rtimes ab,aba,bab,ab\ltimes\} \\ \mathbf{F}_7(\rtimes abab\ltimes) &=& \{\rtimes abab\ltimes\} \\ \end{aligned}\]\(\mathbf{F}_{\leq n}(\cdot)\) returns all of the \(n\)-factors up to and including length \(n\).
\[\mathbf{F}_{\leq n}(s) = \bigcup\limits_{i=1}^{n} \mathbf{F}_{i}(s)\]So, for example, \(\mathbf{F}_{\leq 3}(\rtimes abab \ltimes) = \{\rtimes,a,b,\ltimes\} \cup \{\rtimes a,ab,ba,b\ltimes\} \cup \{\rtimes ab,aba,bab,ab\ltimes\}\).
We can also define a similar function on languages (i.e., sets of strings).
\[\mathbf{F}_{n}(L) = \bigcup\limits_{s \in L} \mathbf{F}_{n}(s)\]So, for example, \(\mathbf{F}_{2}(\{\rtimes aba \ltimes, \rtimes bb \ltimes\}) = \{\rtimes a,ab,ba,a\ltimes\}\cup\{\rtimes b,bb,b\ltimes\}\).
Recognizers: Strictly Local Automata
We first define these languages in terms of a recognizer. In formal language theory, recognizers often take the form of automata, and we will see our first such device here.
A strictly n-local automaton \(\mathcal{A}\) is a pair \(\langle V, T\rangle\) (or, if we want to be explicit, \(\langle V_{\mathcal{A}}, T_{\mathcal{A}} \rangle\)) where \(V\) is our vocabulary as usual and \(T \subseteq \mathbf{F}_n(\{\rtimes\} \cdot V^* \cdot \{\ltimes\})\). In other words, \(T\) is some set of \(n\)-factors over the set of all strings over the vocabulary, with start- and end-string symbols added.
Such tuple-based definitions of formal grammars are common in formal language theory and we will see several more examples. The pair \(\langle V, T \rangle\) is a datastructure which stores the information that distinguishes one strictly-local model from another.
The formal language defined by a strictly \(n\)-local automaton \(\mathcal{A}\) is defined to be.
\[L(\mathcal{A}) = \{s \in V_{\mathcal{A}}^{*} \mid \mathbf{F}_n(\rtimes \cdot s \cdot \ltimes) \subseteq T_{\mathcal{A}}\}\]In other words, the language is set of all strings which start with the start symbol and end with the end symbol and whose \(n\)-grams (\(n\)-factors) are all in the set of valid factors for the grammar. Computationally, we can think of an automaton \(\mathcal{A}\) as sliding a window of width \(n\) over the input string and checking that every \(n\)-factor in string \(x\) is in the set \(T_{\mathcal{A}}\).
Example: Strictly-Local Automaton for \((ab)^n\).
Let’s look at an example of a strictly-local automaton which generates a familiar formal language \((ab)^n\). This language is defined by the following strictly-local automaton:
\[\mathcal{A}_{(ab)^n} = \langle \{a,b\}, \{\rtimes\ltimes,\rtimes a,ab,ba,b\ltimes \}\rangle\]We can visualize the automaton accepting this language like the one in the following diagram. This automaton scans the input string from left to right, checking if each \(n\)-factor in the input string is in the set \(T_{\mathcal{A}_{(ab)^n}} = \{\rtimes\ltimes,\rtimes a,ab,ba,b\ltimes \}\). If every factor in the input is in that set, it accepts; if not, it rejects.
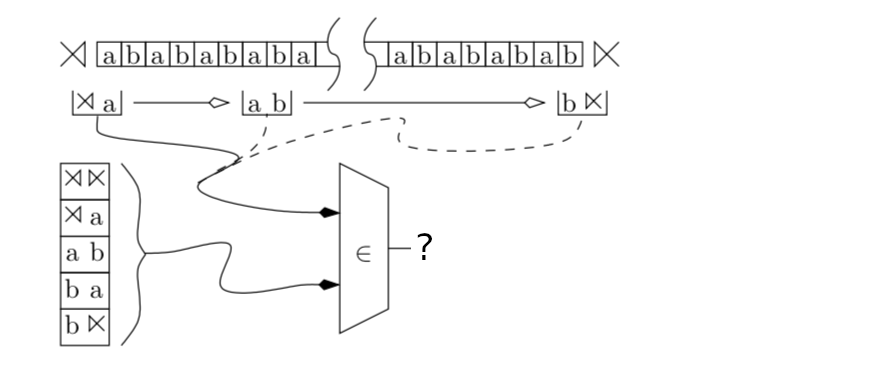
This can captured programmatically in the following way. First, let’s define a predicate which checks to see if a string is a member of a set of \(n\)-factors.
(defn is-factor? [str factors]
(if (empty? factors)
false
(if (= str (first factors))
true
(is-factor? str (rest factors)))))
(list
(is-factor? '(a b) '((a b) (b b)))
(is-factor? '(a a) '((a b) (b b))))
We now define a recognizer for our our language using the take
function which returns the first \(n\) elements of a list when called
like: (take n list).
(defn in-ngram-language? [str n factors]
(if (is-factor? str factors)
true
(if (is-factor? (take n str) factors)
(in-ngram-language? (rest str) n factors)
false)))
(list
(in-ngram-language? '(a b b b) 2 '((a b) (b b)))
(in-ngram-language? '(a b a b) 2 '((a b) (b b))))
Generators: Strictly Local Grammars
As usual, we would also like to characterize a strictly-local language in terms of a generator or grammar. A strictly n-local grammar \(\mathcal{G}\) is a pair \(\langle V, T \rangle\) where \(V\) is our vocabulary and \(T \subseteq \mathbf{F}_n(\{\rtimes\} \cdot V^* \cdot \{\ltimes\})\). As in our definition of an automaton, \(T\) is some set of \(n\)-factors over the set of all strings over the vocabulary, with start- and end-string symbols added.
The formal language defined by a \(n\)-local grammar \(\mathcal{G}\) is defined to be.
\[L(\mathcal{G}) = \{s \in V_{\mathcal{G}}^{*} \mid \mathbf{F}_n(\rtimes \cdot s \cdot \ltimes) \subseteq T_{\mathcal{G}}\}\]In other words, the language is set of all strings that start with the start symbol and ending with the end symbol and whose \(n\)-grams (\(n\)-factors) are all in the set of valid factors for the grammar,
The definitions for strictly \(n\)-local grammars and strictly \(n\)-local automata are essentially identical. However, the way that each system operate and uses the information on an intuitive level is quite different. In the case of the grammars, we imagine an algorithm which makes nondeterministic choices to generate a string, whereas in the case of the automata, we imagine an algorithm which recognizes a string.
Example: Strictly-Local Grammar for \((ab)^n\).
We can think of the generative model for such grammars as consisting of a inventory of \(n\)-grams or \(n\)-factors, given by \(T_\mathcal{G}\) which can be “snapped together” like Lego bricks where \(n-1\) of the symbols on the next brick match the last brick. This is illustrated in the case of a \(2\)-local grammar for the language \((ab)^n\) below.
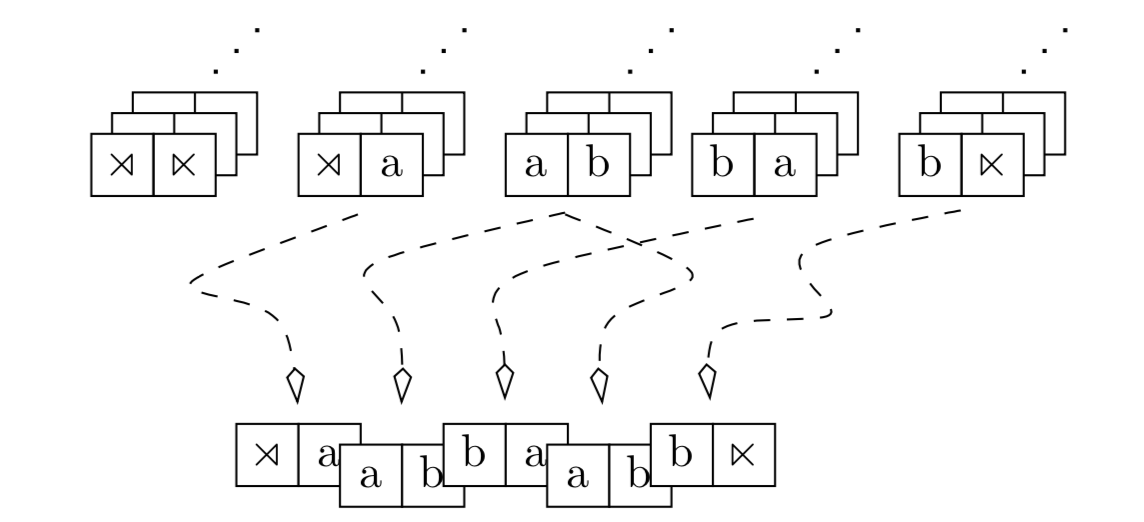
We will not give Clojure code for a generator here since it is more natural to do so in a probabilistic setting so that we do not have to define things in terms of nondeterministic choice.
← 18 Inference Using Conditionalization 20 Strictly-Local Languages, Formal Hierarchies, and Weak Generative Capacity →