(defn logsumexp [& log-vals]
  (let [mx (apply max log-vals)]
    (+ mx
       (Math/log2
	     (apply +
	       (map (fn [z] (Math/pow 2 z))
		    (map (fn [x] (- x mx))
			log-vals)))))))
			
(defn flip [p]
  (if (< (rand 1) p)
    true
    false))

(defn score-categorical [outcome outcomes params]
  (if (empty? params)
    (throw "no matching outcome")
    (if (= outcome (first outcomes))
     (Math/log2 (first params))
      (score-categorical outcome (rest outcomes) (rest params)))))

(defn list-unfold [generator len]
  (if (= len 0)
    '()
    (cons (generator)
    (list-unfold generator (- len 1)))))


(defn sample-gamma [shape scale]
(apply + (repeatedly
  shape  (fn []
		     (- (Math/log2 (rand))))
		)))

(defn sample-dirichlet [pseudos]
  (let [gammas (map (fn [sh]
                     (sample-gamma sh 1))
                pseudos)]
    (normalize gammas)))

(defn normalize [dist]
  (let [sum (apply + (map prob dist))]
    (map
     (fn [x]
       [(value x) (/ (prob x) sum)] )
     dist)))

(defn sample-categorical [dist]
  (if (flip (prob (first dist)))
    (value (first dist))
    (sample-categorical
     (normalize (rest dist)))))


  

In the last chapter, we introduced the parsing as deduction approach to formulating parsers. In this chapter, we show how this approach can use used to solve all of the parsing problems we have formulated in this book: the recognition problem, finding the maximum likelihood derivation, and marginalizing over derivations to find the probability of the string.

Amazingly, all of these problems can be solved by the same exact algorithms! The key to unifying these algorithms is to introduce the notion of a semiring. A ring refers to a mathematical object \(\langle A, \oplus, \otimes, 0, 1 \rangle\) which consists of a set \(A\) and two operations \(\oplus\) and \(\otimes\), and an identity for \(\oplus\), \(0\) and an identity for \(\otimes\) \(1\). This structure corresponds to normal additiona and multiplication except that we don’t assume that addition has an inverse (i.e., there are no negative numbers). In other words, these operations satisfy the following axioms.

\[\begin{align} (a \oplus b) \oplus c &= a \oplus (b \oplus c) &|& \ \mathrm{Associativity~of~addition} \\ 0 \oplus a &= a &|&\ \mathrm{Identity~for~addition} \\ a \oplus b &= b \oplus a &|&\ \mathrm{Commutativity~of~addition} \\ (a \otimes b) \otimes c &= a \otimes (b \otimes c) &|&\ \mathrm{Associativity~of~multiplication} \\ 1 \otimes a &= a &|&\ \mathrm{Identity~for~addition} \\ a \otimes (b \oplus c) &= (a \otimes b) \oplus (a \otimes c) &|&\ \mathrm{Left~distributivity~of~multiplication~over~addition} \\ (a \oplus b) \otimes c &= (a \otimes c) \oplus (b \otimes c) &|&\ \mathrm{Right~distributivity~of~multiplication~over~addition} \\ 0⋅a &= 0 &|&\ \mathrm{Multiplicative~annihilator} \end{align}\]

An example of a semiring is the real numbers with the usual definitions of addition and multiplication \(\langle \mathbb{R}, +, \times, 0, 1 \rangle\). However, there are more interesting semirings. For instance, the boolean semiring is the semiring \(\langle \{ 1, 0 \}, \vee, \wedge, 0, 1 \rangle\). The Viterbi semiring is \(\langle \mathbb{R}_{0}^{1}, \mathrm{max}, \times, 0, 1 \rangle\) and the Inside semiring is given by \(\langle \mathbb{R}_{0}^{\infty}, +, \times, 0, 1 \rangle\)

Here is semiring parsing applied to CYK.

---

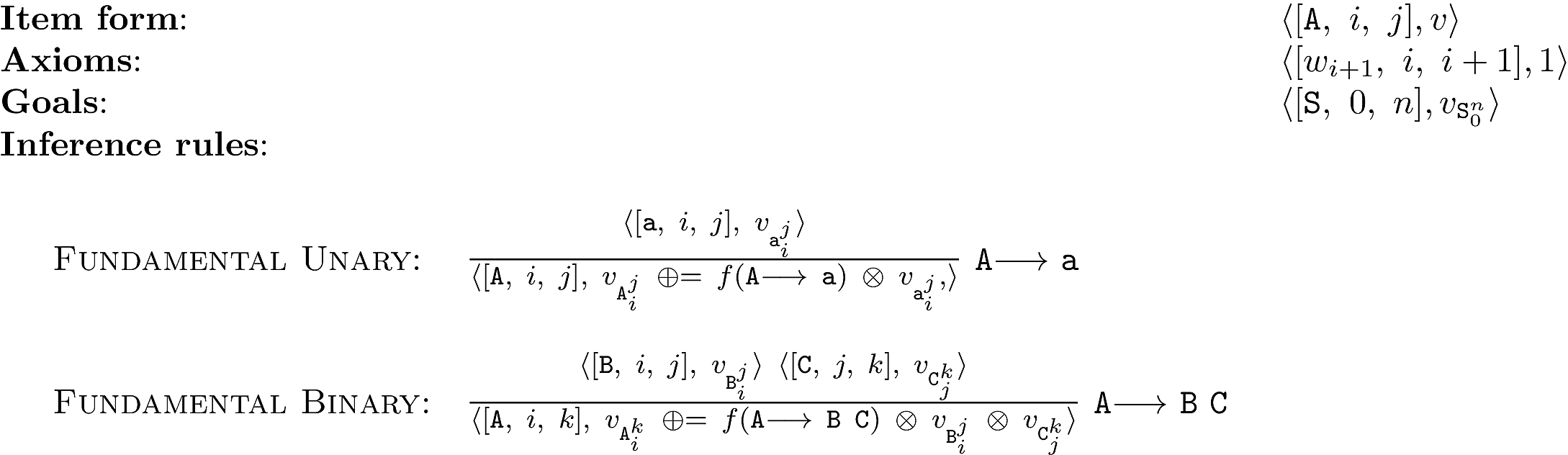
← 45 Chomsky Normal Form and CYK Parsing 47 Viterbi and Inside Parsing for CFGs →