(def categories '(N V Adj Adv P stop))

(def vocabulary '(Call me Ishmael))

(defn logsumexp [& log-vals]
  (let [mx (apply max log-vals)]
    (+ mx
       (Math/log2
	     (apply +
	       (map (fn [z] (Math/pow 2 z))
		    (map (fn [x] (- x mx))
			log-vals)))))))
			
(defn flip [p]
  (if (< (rand 1) p)
    true
    false))

(defn sample-categorical [outcomes params]
  (if (flip (first params))
    (first outcomes)
    (sample-categorical (rest outcomes)
                        (normalize (rest params)))))

(defn score-categorical [outcome outcomes params]
  (if (empty? params)
    (throw "no matching outcome")
    (if (= outcome (first outcomes))
     (Math/log2 (first params))
      (score-categorical outcome (rest outcomes) (rest params)))))

(defn normalize [params]
  (let [sum (apply + params)]
  (map (fn [x] (/ x sum)) params)))

(defn sample-gamma [shape scale]
(apply + (repeatedly
  shape  (fn []
		     (- (Math/log2 (rand))))
		)))

(defn sample-dirichlet [pseudos]
  (let [gammas (map (fn [sh]
                     (sample-gamma sh 1))
                pseudos)]
				(normalize gammas)))

(defn update-context [order old-context new-symbol]
  (if (>= (count old-context) order)
    (throw "Context too long!")
    (if (= (count old-context) (- order 1))
      (concat  (rest old-context) (list new-symbol))
      (concat old-context (list new-symbol)))))

(defn hmm-unfold [transition observation order context current stop?]
  (if (stop? current)
    (list current)
    (let [new-context (update-context
	           order
		       context
		       current)
	        nxt (transition new-context)]
	  (cons [current (observation current)]
	  (hmm-unfold
	         transition
	         observation
	         n-gram-order 
			 new-context
			 nxt
			 stop?)))))

(defn all-but-last [l]
  (cond (empty? l) (throw "bad thing")
        (empty? (rest l)) '()
        :else (cons (first l) (all-but-last (rest l)))))

In Parsing as Deduction, we introduced a general framework for expressing different parsing algorithms as systems of logical deduction and in Semirings we showed how to organize different parsing problems (recognition, maximization, marginalization) by considering the parsing problem over different semirings. However, we have not discussed how these two idea can be used in a practical parsing algorithm. In this unit, we introduce a general way of using a parsing as deduction system known as chart parsing.

The idea of chart parsing is to keep track of two datastrcutures. First, the chart stores all of the items that have been discovered (i.e., proven) by the algorithm. The second datastructure, the agenda keeps track of which items should be used to generate later deductions using the inference rules.

The general procedure looks like this:

1. Initialize an empty chart and put the axioms of the parsing as deduction system into the agenda.
2. While there is anything in the agenda, repeat the following steps.
   1. Take a trigger item off of the agenda.
   2. If the trigger item is not in the chart already.
      1. Add it to the chart.
      2. Generate all items that result by applying the deduction rules to the trigger item and other items already in the chart.
      3. Add all these generated items to the agenda.
3. If the goal item is in the chart, then it contains the answer to the parsing problem as it’s semiring value component.

In order to understand the notion of a trigger, it is useful to consider the CYK algorithm.

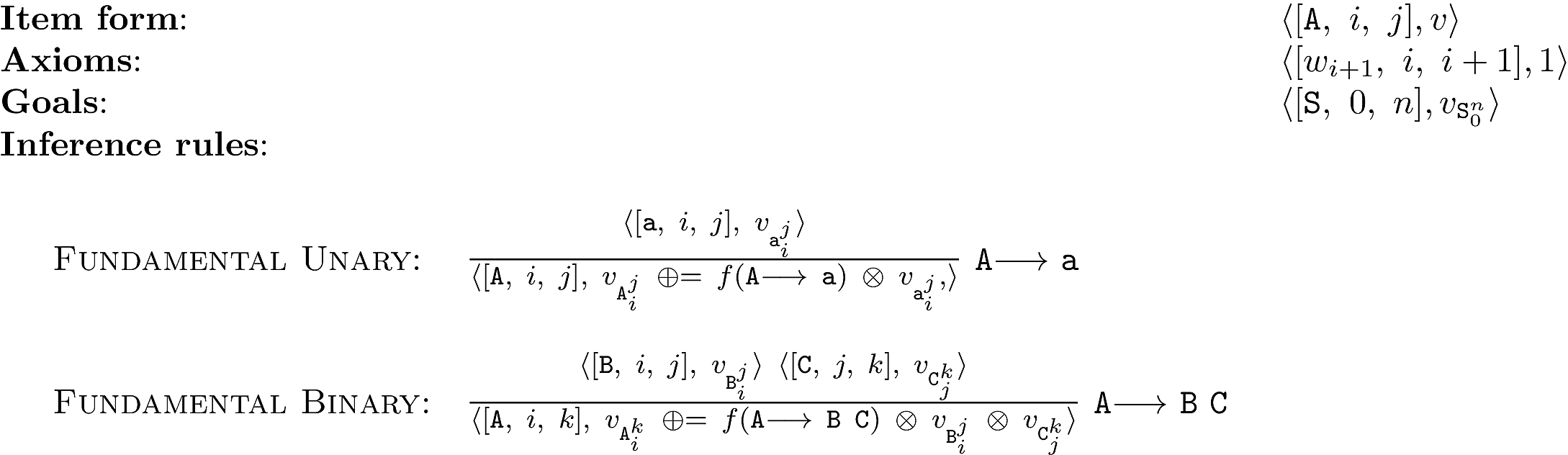
Each of the two rules has its own kind of trigger(s). The first rule is triggered by taking an item off the agenda that has a terminal in it. incomplete item is triggered by taking a complete item off of the agenda. It will generate new incomplete items which will be added to the agenda.

The second rule advance incomplete item is triggered either by taking an incomplete item off of the agenda. In this case the incomplete item will look for every complete item that is in the chart that can appear to the right and introduce a new incomplete item into the agenda, with the dot advanced. This rule can also be triggered by a complete item on the right. In this case, the complete item will find every incomplete item that ends in the correct place and introduce the resulting edges to the agenda.

Finally, the final rule is triggered by an incomplete item whose dot is at the far right of the rule. In this case, the rule will introduce a complete item into the agenda.

For this to work efficiently, we must order the search such that smaller items are built before larger items. This can be accomplished by making the agenda a priority queue which always returns the item whose span (i.e., \(j-i\)) is as short as possible.

Finally, we need to be careful not to double count ways of building item produced by the second rule. This can happen, for instance, we we trigger the second rule two times with the same inputs by adjacent incomplete and complete item of the same length. To guard against this, we can implement a check that we only allow incomplete triggers to apply when the complete item to the right is stricter shorter than the incomplete item on the left.

---

← 47 Viterbi and Inside Parsing for CFGs 48 Parameter Estimation for CFGs →