In the last chapter, we saw how lists can be built using the list constructor or by quoting. But there is a more useful and fundamental way to think about the structure of lists which we will make extensive use of in this course.

We can represent a list as a sequence of applications of the cons procedure, starting from the empty list: (cons 1 (cons 2 (cons 3 '()))

(list 1 2 3)

(cons 1 (cons 2 (cons 3 '())))

So (list 1 2 3) can be built by applying cons to the value 1 and another list (2 3); this latter list can be built by applying cons to the value 2 and another list (3), and so on, with the last element in the sequence being the empty or null list ().

We can use first and rest to navigate around this list.

(first (list 1 2 3))

(rest (list 1 2 3))

The structure of lists is important because it goes hand in hand with the most important code design pattern used in the \(\lambda\)-calculus and functional programming: recursion. We can process a list by defining a function which does something to the first element of the list, and calls itself recursively on the rest of the list. The base case of such a recursive list processing procedure is the empty list ().

Recursion is best explained with an example. One extremely important and basic list-processing function that exists in all functional languages is known as map. map is a higher-order function which takes two arguments: (map f l). Its first argument is a one-place (single argument) procedure f and its second second is a list l. The function map returns the list that results from applying f to each element of l.

(map (fn [x] (+ x 1) ) '(1 2 3 4 5 6))

In the example above, we called map with two arguments. First, we passed in an anonymous function (fn [x] (+ x 1)) which simply adds one to whatever it is passed as an argument. Second, we passed in the list (1 2 3 4 5 6). map applied the anonymous function to each element of the list and returned the resulting list (2 3 4 5 6 7).

map is a standard function in all functional programming languages because it is a common use case for iteration. But it is easy to define it ourselves using recursion.

(defn my-map [f l]
  (if (empty? l)
    '()
    (cons (f (first l))
          (my-map f (rest l)))))

(my-map (fn [x] (+ 1 x)) '(1 2 3 4 5 6))

Let’s go through this function definition. First, the function takes two arguments: a function f and a list l. The body of the procedure is a conditional. This conditional first checks if the list l is the empty list using the built in procedure empty?. If the list passed to my-map is empty, then the result must also be empty, so we set the value of the conditional to just the empty list. On the other hand, if there are elements in the list l, we need to do more work.

The alternative to the conditional first gets the first elements of l with first, i.e., (first l) and it then applies the function f to this element. Second, it calls itself on the remainder of the list which it gets using rest. Finally, it takes the result of these two operations and creates a pair from these using cons.

Let’s look at another example of recursion.

(defn sum [l]
  (if (empty? l)
    0
    (+ (first l) 
       (sum (rest l)))))

(sum '(1 2 3 3 4))

This function takes a list of numbers, and returns the sum of those numbers. The recursion in this definition says something very simple (but important) about summing a list: the sum of a list is equal to the first number in the list plus the sum of the rest of the list.

In both of these examples, we saw the same pattern for recursing on the structure of a list.

(defn rec-fun [l]
  (if (empty? l)
    base-case
    (accumulate (do-something (first l))
                (rec-fun (rest l))))) ; <- recursive call

This is a very general pattern. The conditional has two parts, when there is nothing in the input list, it returns some base case. For instance, in the map example this is () and in the sum example it is 0. Otherwise, the function peels off the first element of the list, does something to it, recurses on the rest of the list, and then accumulates the two results.

We can use this observation to write a higher order function that generates a such recursive functions, given the base case, accumulator, and an operation to apply to each element of the list before recursing.

(defn make-rec-fn [base-case accumulate operation]
  (fn rec-fun [l]
    (if (empty? l)
      base-case
      (accumulate (operation (first l))
                  (rec-fun (rest l))))))

Recursion and trees

How are recursively defined functions executed? One helpful way to visualize recursion is using a tree.

(sum '(1 2 3))

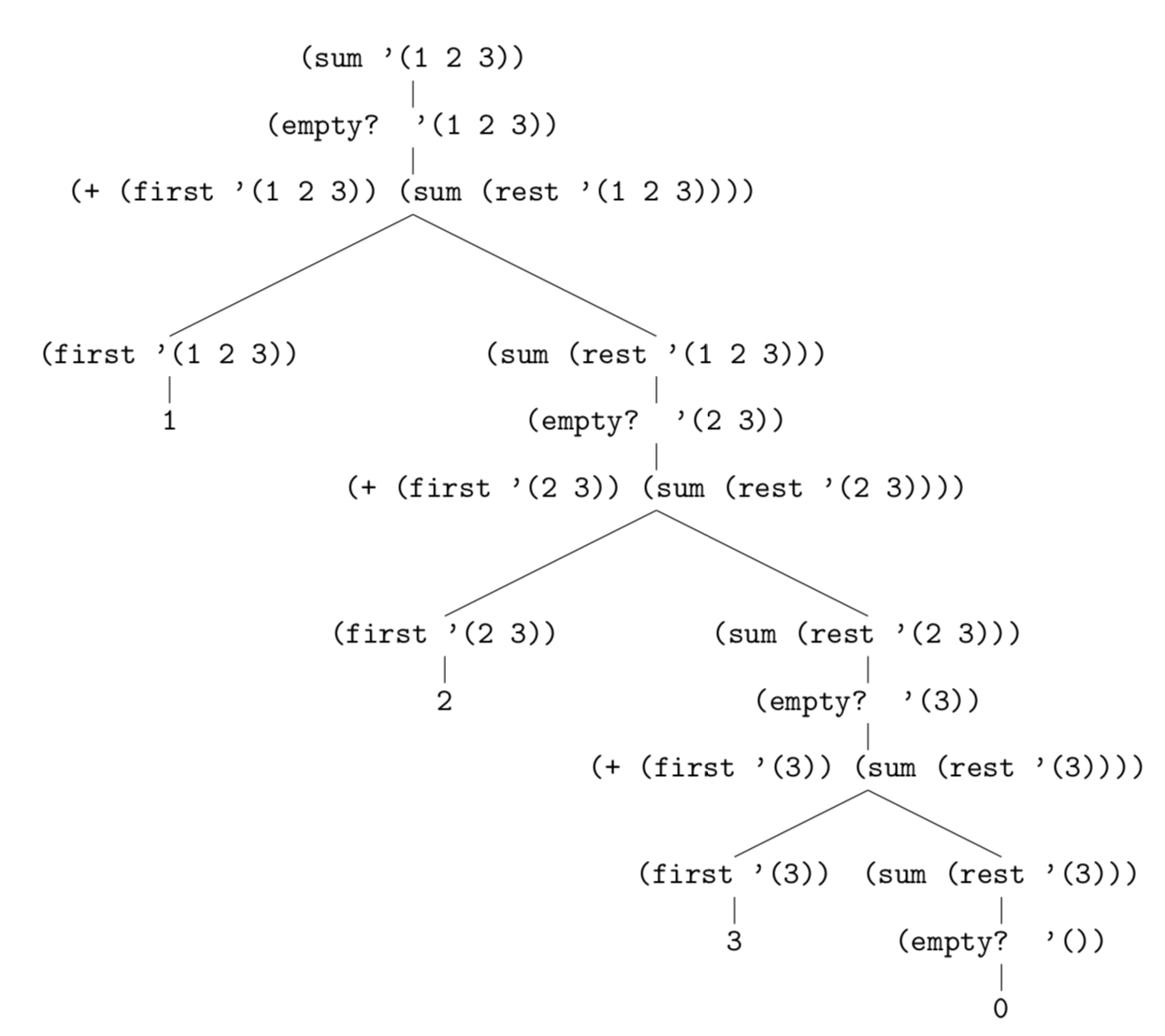
When first working through recursive functions it is often helpful to explicitly walk through the tree structure of the computation. In linguistics, we usually make extensive use of such trees which we usually call derivation trees or parse trees. Although they are not usually presented in terms of computation traces, they are often best thought of as such.

Two ways to think about recursion

The discussion above illustrates two different but complementary ways to think about recursion.

1. The procedural view considers how a recursive function is computed step-by-step and is best understood by thinking of the tree of recursive calls, like the one we drew above.

2. The declarative view considers how the recursive function is defined “by contract”—we break the definition into cases and define the correct behavior for each case. In the base case we define the output behavior directly in terms of the input. In the inductive case, we make the assumption that the function (e.g.,sum or map), is defined correctly on smaller/simpler inputs (i.e., (sum (rest l)) or (map f (rest l))) and define the relationship between those smaller/simpler inputs and the full input (i.e., (sum l) or (map f l)).

The declarative view can be unintuitive at first, since it relies on a sort of leap-of-faith-style reasoning process. The inductive cases require that we call our function as if we believe that it was already correctly defined. However, this kind of inductive reasoning is a powerful tool in programming (and mathematics more generally); so, it is worth understanding deeply.

← 2 Models of Computation 4 Well-Formed Sentences and Grammaticality →